I recently gave a talk at a seminar course (Invitation To Combinatorics), where i was so lucky as to get to talk about the Riemann-Roch theorem for graphs! The theorem and all the underlying theory is marvalous and the analogy to algebraic geometry is really something.

What more the theorem need not much mathematical knowledge to state nor to be interesting. Indeed, it turns out to have a super nice analogy in a simple game anyone can play one graphs!

You can find my notes for the talk, with all the nitty gritty details, here.

The Dollar Debt Game

The easy and fun analogy, which is often given, is that of the dollar debt game.

Say we have a network of people. If two people are friends we connect them with an edge. (In graph theoretic terms, we call the network a graph and the people the vertices . We denote by \(V(G)\) the set of vertices, and \(E(G)\) the set of edges in a graph, \(G\)).

Each person has some amount of money or debt, represented naturally by an integer. We wish to exchange money in such a way that no-one is in debt. However, a person may only either receive 1 dollar from every friend or give 1 dollar to every friend. For example, the following is a valid move.

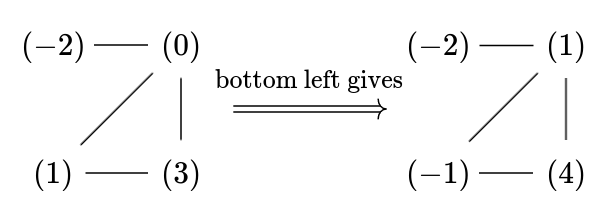
Naturally we ask. When can we win the game?

For starters we know that there has to be at least as many dollars on the board as there are people. However, even when there is more money than people it may still be unwinnable! Consider the configuration below:

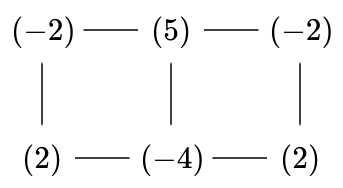
Try as you might, you cannot win, even though there are only 6 people and a surplus of money.

In fact, it turns out the genus of the graph has a say in when the game is winnable: Recall the genus is defined as \(g := |E(G)| - |V(G)| + 1\). The genus of a graph can be thought of as a way to measure the ‘interconnectedness’ of the graph, the higher, the more interconnected. One can also think of it in topological terms, as the number of holes in the graph. (For example the graphs above have 1, respectively 2 holes).

If we now denote the total number of dollars on the board, \(D\), by \(\deg(D)\). Then it turns out we know exactly for which graphs and amounts of money, this game is always winnable.

Theorem If \(\deg(D)\ \geq g\), then the game is always winnable. Furthermore, if \(\deg(D) \leq g -1\), then there exists some configuration for which the game is not winnable.

While this is an amazing result on its own, we can, in fact, say even more!

However, first we must introduce some more definitions.

If we define by \(r(D)\) to be \(-1\) if the game is not winnable and otherwise to be the maximum number of dollars we may remove without it becoming unwinnable. We also denote by \(K\), the canonical configuration, which assigns to each vertex, \(v\), \( \text{deg}(v)-2 \) dollars, where \(\text{deg}(v)\) is the number of edges \(v\) has. Then we have the following relation. Those familiar with algebraic geometry will certainly recognize this as Riemann-Roch!

Theorem (Riemann-Roch for graphs) On any board, \(D\), on any graph, \(G\), we have that

$$ r(D) - r(K-D) = \deg(D) + 1 - g. $$

The tie to algebraic geometry goes much much deeper than this, and i suggest anyone whose interest has been peaked to refer to the notes LINK.

Application: Volumetric Kirchoff’s theorem

Many will be familiar with Kirchoff’s theorem.

Theorem (Kirchhoff’s Theorem) The number of spanning trees of a graph, \(G\), is equal to any cofactor of the Laplacian of \(G\).

However, in the context of the algebraic geometry which one finds in the notes, we can state Kirchoff’s theorem in a whole different context which admits a volumetric addition to the theorem.

DEFINTION DEFINTION DEFINITION

(Maybe just picard, pricipal, and break divisors?)

THEOREM

Example

EXAMPLE